Solving the XKCD NP-Complete Restaurant Order Problem with Python and Optlib
Introduction to Optimization Problems
If you ever find yourself looking for the minimum (or equivalently the maximum) of a function value, you have an optimization problem.
For continuous functions we can use calculus to provide analytical guidance for minima. As an example, for a single variable function, the point of inflection of a double derivative will highlight a local minima. You may remember solving these problems in calculus classes finding the minima or maxima of parabolas.
With discrete values, we lose the analytical guidance provided over continuous functions. Our functions are no longer differentiable as there are discontinuities between points.
Discrete optimization problems exist in everyday life and vary in complexity to solve. They could be something as simple as given a list of gas stations pick the one that is the cheapest or as complex as pick an investment portfolio that will minimize risk.
Some optimization problems can be easy to solve with a few assumptions. For example if we have a list of gas stations and want to minimize price, we could add the assumption that driving distance doesn’t matter when picking a gas station. In this case the optimal gas station is simply the one with the minimum price. If the list of gas stations was filtered to be ones that were acceptable to drive to, this would provide a reasonable solution. However if you are solving this problem on massive scale, you may want to model driving time and distance costs in the optimization. Pinching pennies at scale easily pays the salaries of many employees :)
There is much art to choosing simplifying assumptions that allow for problems to be tractable. The hardest place for optimization problems to solve properly is when the system is discrete with many combinations of state. One particularly famous family of functions with discrete integer values can be optimized with a technique called “Integer Linear Programming”.
Integer Linear Programming
Any function that can be written as a combination of a weight multiplied by an integer value can be minimized with Integer Linear Programming (ILP). While in general integer programming problems are NP-complete, smart people have created optimization packages that can find good and sometimes even optimal solutions.
For these sorts of optimization problems, there will be constraints placed on a solution that bound what is considered an acceptable solution. Constraints can come from many places such as physical constraints of realizable solutions or desired properties such as profit is greater than cost.
Solving the XKCD Restaurant Order Problem - Deliciously
XKCD has a comic funny for us nerds, painful for everyone else, about embedding optimization problems in restaurant orders:
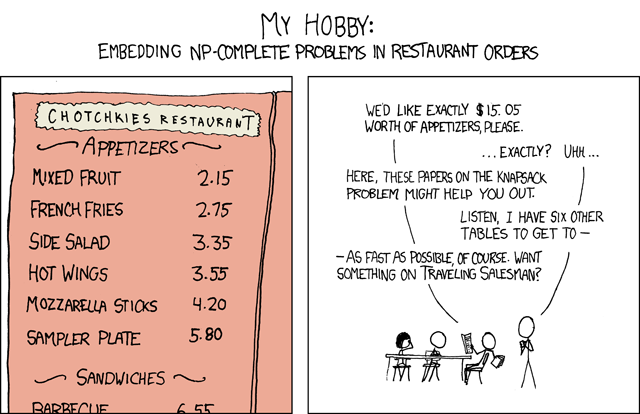
The XKCD optimization problem is this: given the prices of several foods, find the sum of elements that equals 15.05:
| Food | Cost |
|---|---|
| Mixed Fruit | 2.15 |
| French Fries | 2.75 |
| Side Salad | 3.35 |
| Hot Wings | 3.55 |
| Mozzarella Sticks | 4.20 |
| Sampler Plate | 5.80 |
We can use an integer programming solver to help our poor server find an optimal solution.
For this instance there are actually multiple solutions that optimally satisfy the constraints. One solution is simply to have 7 orders of mixed fruit. However that order is not very diverse and way too healthy for the typical person. Let’s make it more delicious!
We can add some fun while still staying within the realm of integer linear programming. Let’s say that we want to find the combination of foods that at the same time minimizes healthiness. Wait minimize healthiness? That’s right - for the most delicious meal, we want to minimize healthiness. This is simply because unhealthy food tastes better - visit New Orleans if you don’t believe me.
To do this, let’s score each food with a healthy index, where 0 is deathly healthy and 10 is necessary for a healthy life:
| Food | Healthy Index |
|---|---|
| Mixed Fruit | 8 |
| French Fries | 3 |
| Side Salad | 7 |
| Hot Wings | 4 |
| Mozzarella Sticks | 2 |
| Sampler Plate | 3 |
We can then compute the total health-food score by summing the product of the number of fruit items and the cost:
Additionally we will ask our solver to add the constraint that everything adds up to $15.05:
\[\$15.05 = \sum_{i \in food} count_i * cost(i)\]Notice that the health, like cost, is simply a constant because we have a numerical value that is unique for each food defined in the tables above.
Solving Integer Programming Problems with Optlang in Python
Before diving into the code there are a several programming primitives important to understand with optlang:
Variables: objects that represent symbolic variables. Under the scenes, optlang uses sympy to provide these symbolic objects. They can have the domain specified, such as integer or real, or bounds specified, like if a variable must be positive then specify the lower bound is 0.Objectives: the function to minimize.Constraints: the boundaries a solution must exist within, defined as a combination of variables and equality operators.Models: containers that compose objectives and constraints.
Now let’s pick the foods that provides the most delicious meal that satisfies our constraint to be equal to $15.05:
from optlang import Variable, Objective, Model, Constraint
costs = {
"mixed_fruit": 2.15,
"french_fries": 2.75,
"side_salad": 3.35,
"hot_wings": 3.55,
"mozzarella_sticks": 4.20,
"sampler_plate": 5.80
}
healthy_index = {
"mixed_fruit": 8,
"french_fries": 3,
"side_salad": 7,
"hot_wings": 4,
"mozzarella_sticks": 2,
"sampler_plate": 3
}
v_is = []
for item, cost in costs.items():
v_i = Variable("%s" % item, lb=0, type="integer")
v_is.append(v_i)
total_cost = sum([v_i * costs[v_i.name] for v_i in v_is])
total_healthiness = sum([v_i * healthy_index[v_i.name] for v_i in v_is])
objective = Objective(total_healthiness, direction="min")
constraint = Constraint(total_cost, lb=15.05, ub=15.05)
model = Model(name="xkcd server model")
model.objective = objective
model.add([constraint])
status = model.optimize()
print(f"optimization status: {model.status}")
print(f"objective value: {model.objective.value}")
cost = 0.0
for name, variable in model.variables.items():
value = int(variable.primal)
print(f"{name}={value}")
cost += costs[name] * value
print(f"total cost: {cost}")
The solution for this is to pick only 1 mixed fruit, 1 sampler plate, and 2 orders of hot wings. That sounds very delicious to me.
This post was originally drafted January 2015, but updated for posting in 2021.